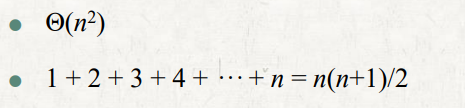[Algorithm] Dynamic Programming (2) - Rod Cutting
1. rod - cutting problem 이란
rod-cutting 이란 전체 길이 n인 막대와 길이 별 가격이 주어졌을 때, 해당 막대를 잘라서 얻을 수 있는 최대수익을 r_n을 구하는 문제이다.
brute-force approach 를 사용하면 2^(n-1)의 possible way를 전부 계산해야 한다.
길이가 n인 막대는 n-1번의 자를 수 있는 틈이 있고, 각각의 틈에는 자른다vs자르지 않는다의 경우가 있기 때문에 2^(n-1)개의 possible way가 있다.


2. 동적 프로그래밍을 이용해서 rod - cutting problem 해결하기

위 그림을 통해 rod - cutting problem을 해결하기 위한 동적 프로그래밍을 이해할 수 있다.
- p_1 + r_n-1 식은 길이가 1일 때 가격 + 길이가 n-1일 때 최대수익을 의미한다.
- p_1, p_2,,, p 까지 n가지의 경우를 확인하고 최종적으로 r_n을 구할 수 있다.

rod - cutting problem을 해결하기 위한 동적 프로그래밍 식을 간단하게 표현하면 다음과 같이 쓸 수 있다.
혹시 이 식이 이해가 안된다면 간단하게 확인해 볼 수 있다.

- p_1 + r_3 일 때 : (b), (e), (f), (h) 를 살펴볼 수 있음.
- p_2 + r_2 일 때 : (c), (g)를 살펴볼 수 있음.
- p_3 + r_1 일 때 : (d) 를 살펴볼 수 있음
- p_4 + r_0 일 때 : (a) 를 살펴볼 수 있음.
- r_n = max (p_i + r_n-i) 를 통해 possible way를 전부 살펴 볼 수 있음을 간단하게 확인할 수 있다.
r_n = max (p_i + r_n-i) 식이 rod - cutting problem을 풀 수 있다는 것을 이해했으면, 해당 식을 통해 어떻게 rod - cutting 문제를 푸는지에 대해 알아보자.
Assembly - line scheduling 문제처럼 우리는 표를 통해 rod - cutting problem을 정리 할 수 있다.


r[i]를 통해 주어진 막대의 길이에 따른 최대수익을 확인할 수 있다.
- EX ) 막대의 길이가 8일 때 최대수익은 22이다.
s[i]를 통해서는 최대수익을 얻으려면 어떻게 막대를 잘라야 하는지 알 수 있다.
- EX ) 막대의 길이가 8일 때 최대수익을 얻는 cutting는 2 + 6이다.
- i가 8일 때, s[8]은 2로, 2 + 6 형태이다. 2는 s[8]에서 구한 값이기 때문에 변하지 않지만, 6은 최대값을 확인해야 한다.
- i가 6일때, s[6]은 6으로 6 + 0 형태이다.
- 그러므로 막대의 길이가 8일 때 최대수익을 얻는 cutting은 2 + 6 이다.
3. rod - cutting problem 수도코드


4. rod - cutting problem의 Space Consumption & Running Time
- Space Consumption

- Running Time