2022. 10. 25. 03:22ㆍ카테고리 없음
1. 알고가야할 정의
- Character :a,b,0,1과 같은 문자
- String ( Sequence ) : A list of characters
- {0,1,1} : Binary string
- {A,C,G,T} : DNA sequence
- Substring vs Subsequence vs Common Subsequence

- The i th prefix X_i of X : 앞에서부터 i번째까지 sequence X의 접두사
- EX ) X = A B C B D A B
- X_4 = A B C B
- EX ) X = A B C B D A B
2. Longest Common Subsequence(LCS)란
X = A B C B D A B & Y = B D C A B A
가 주어졌을 때, B C B A 와 같이, 가장 긴 공통 부분 수열을 의미한다. 부분수열이기 때문에 공통되지 않은 다른 문자는 건너뛰어서 공통된 문자를 찾을 수 있다.
Brute force approach : X의 모든 부분수열을 열거한 후, 각각의 수열이 Y의 부분수열인지 확인한다. 그 후 확인된 공통된 부분수열 중 가장 긴 것을 선택한다.
Brute force approach로 possible way를 전부 확인한 수 LCS를 찾는 방법은 불가능한다. 길이가 m인 string X의 부분수열은 2^m개이기 때문이다.
3. Longest Common Subsequence(LCS)의 동적 프로그래밍
Brute force approach가 불가능하기 때문에 동적 프로그래밍을 활용해야 한다.

X의 마지막 character하고 Y의 마지막 character하고 같은 경우, Z_(k-1) 은 LCS( X_(m-1), Y_(n-1) )을 다시 계산해서 구할 수 있다. 그러니까 위에 sequence는 마지막 character이 B로 같으니까 이제 X = A B C B D A 하고 Y = B D C A 를 통해 마지막 char B 이전에 공통된 char을 찾으면 된다.

X의 마지막 character하고 Y의 마지막 charcater하고 같지 않은 경우, X_(m-1)과 Y_n을 비교하거나, X_m 과 Y_(n-1)을 비교해서 한 단계 이전의 LCS를 찾는다. 그러니까 위에 sequence에서 마지막 character이 같지 않으니 X = A B C B D A 와 Y = B D C A A 를 비교하거나 혹은 X = A B C B D A B 와 Y = B D C A 를 비교한다.
다른 동적 프로그래밍과 마찬가지로 LCS도 표를 그려 본다.


i와 j가 모두 0이 아닌 경우, 저 핑크색 사각형을 참고하여 표를 채워나간다.
- C[2][3]을 채우기 위해 X_2와 Y_3을 비교해야한다. X_2는 B이고, Y_3은 C로 같지 않기 때문에, LCS( X_(m-1), Y_n )와 LCS( X_m , Y_(n-1) ), 그러니까 저 연두색 사각형 중 큰 걸 선택해서 C[2][3]을 채워넣는다.
- 만약 X_2와 Y_3가 같았다면, LCS( X_(m-1), Y_(n-1) )에 +1을 해야하기 때문에, 하늘색 사각형에 해당하는 숫자 +1을 해서 C[2][3]을 채운다.
4. Longest Common Subsequence(LCS)의 수도코드


5. Multiple LCSs
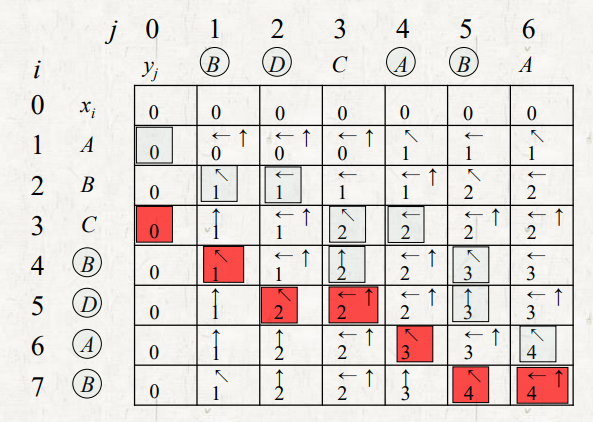
X_i와 Y_j가 같지 않을 때, LCS( X_(m-1), Y_n )와 LCS( X_m , Y_(n-1) )중에 큰걸 골라서 C[i][j]를 넣어야 하는데, LCS( X_(m-1), Y_n )와 LCS( X_m , Y_(n-1) )이 같을 때도 있다. 일반 LCS에서는 그냥 아무거나 넣는데, Multiple LCSs 에서는 둘 다 표시한다.



6. Longest Common Subsequence(LCS)의 Space Consumption & Running Time
- Space consumption



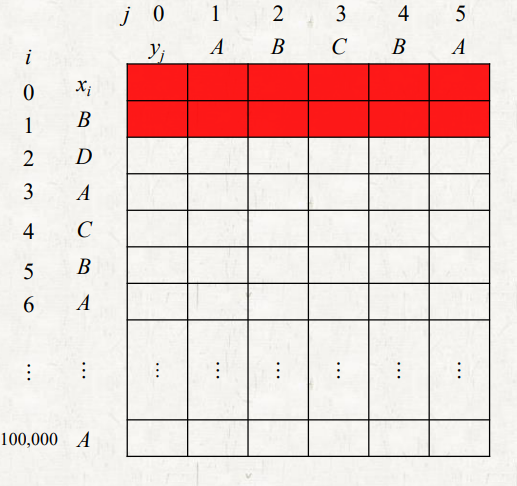
- 왼쪽 테이블과 같이 2 rows만으로 LCS length를 계산할 수 있다.
- columns가 길면 x,y축을 바꿔서 rows를 길게 만들면 되기 때문에, min(m,n)이 가능하다.
- Running Time
